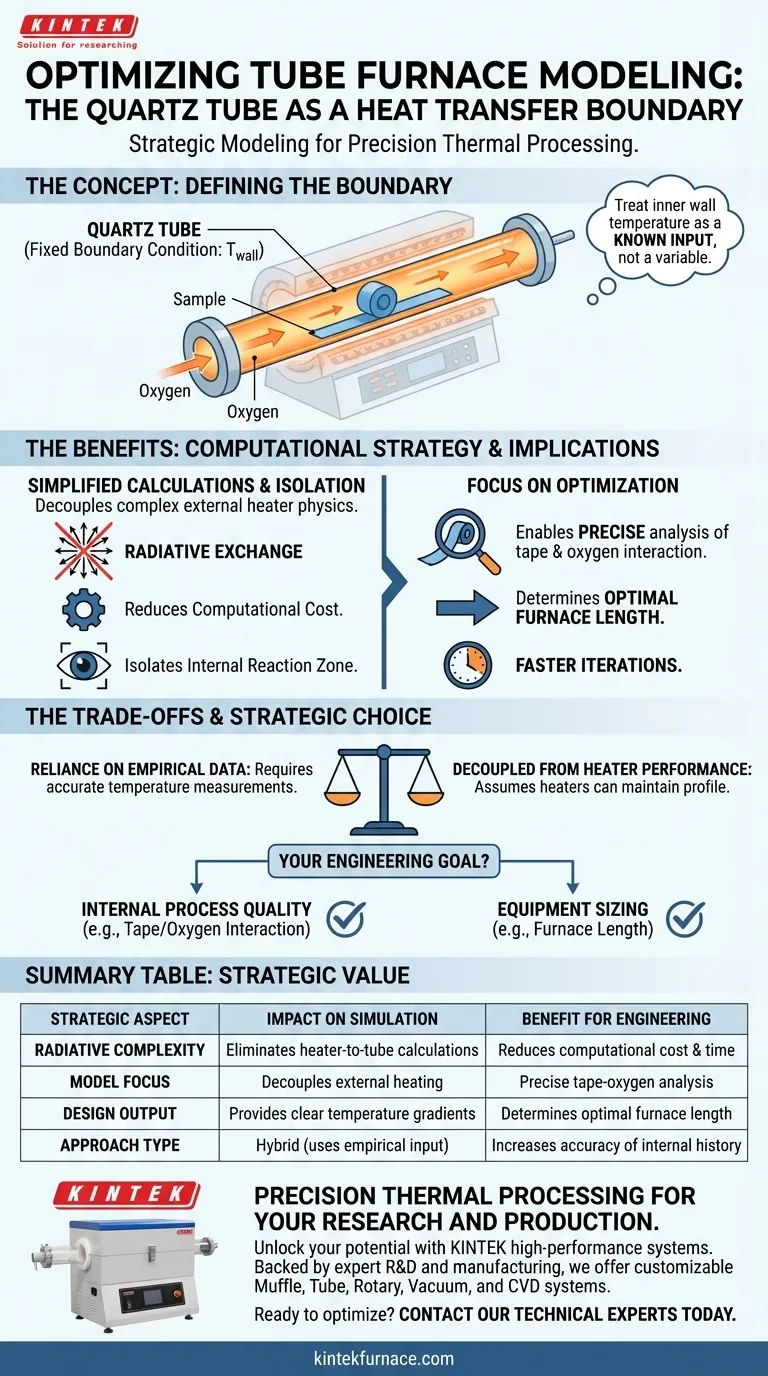
Definire il tubo di quarzo come condizione al contorno per il trasferimento di calore è una decisione di modellazione strategica che isola il processo interno dalle variabili esterne. Trattando la distribuzione della temperatura della parete interna come un input noto anziché una variabile da risolvere, si disaccoppia la complessa fisica degli elementi riscaldanti esterni dalla zona di reazione interna. Ciò semplifica notevolmente il modello matematico eliminando la necessità di calcolare lo scambio radiativo tra i riscaldatori e il tubo.
Concetto chiave: trattare la temperatura della parete interna del tubo di quarzo come una condizione al contorno fissa riduce drasticamente la complessità computazionale. Ciò consente di bypassare i calcoli di radiazione esterni e concentrarsi interamente sul trasferimento di calore critico tra il nastro e l'ossigeno fluente, consentendo un'ottimizzazione precisa della lunghezza del forno.
La strategia computazionale
Semplificare i calcoli radiativi
Il trasferimento di calore radiativo è computazionalmente costoso a causa della sua natura non lineare e della complessità geometrica.
In un modello di forno completo, si calcolerebbe tipicamente come gli elementi riscaldanti irradiano energia al tubo di quarzo. Tuttavia, misurando la distribuzione effettiva della temperatura della parete interna del tubo di quarzo e applicandola come condizione al contorno, si bypassano completamente questi complessi calcoli.
Isolare la zona di reazione
Il tubo di quarzo funge da "vaso centrale" che media lo scambio di calore.
Definendo la sua superficie interna come confine, si sposta l'attenzione della simulazione. Il modello non si preoccupa più di *come* il tubo si scalda; si preoccupa solo di come il tubo trasferisce quel calore ai componenti interni. Ciò crea un'analisi mirata dell'ambiente circostante il nastro campione.
Implicazioni per l'ottimizzazione del design
Concentrarsi sull'interazione nastro e ossigeno
Una volta impostato il confine, il modello può dedicare le sue risorse alla fisica interna.
È possibile analizzare esplicitamente il comportamento del trasferimento di calore tra il nastro campione e l'ossigeno fluente. Ciò rivela come si sviluppano i gradienti di temperatura nel flusso di gas e con quale efficacia il calore viene trasferito alla superficie del nastro.
Ottimizzare la lunghezza del forno
Il beneficio pratico finale di questo approccio di modellazione è l'ottimizzazione geometrica.
Comprendendo i tassi specifici di trasferimento di calore tra la parete del tubo, l'ossigeno e il nastro, è possibile determinare esattamente quanto tempo il nastro deve rimanere nella zona calda. Ciò informa direttamente la lunghezza di progettazione necessaria del forno per garantire un'adeguata lavorazione termica.
Comprendere i compromessi
Affidamento sui dati empirici
Questo metodo non è una simulazione "pura"; è un approccio ibrido.
Richiede distribuzioni di temperatura accurate e pre-misurate della parete interna del tubo di quarzo. Se le misurazioni di input sono imprecise o a bassa risoluzione, i risultati della simulazione saranno ugualmente errati.
Disaccoppiamento dalle prestazioni del riscaldatore
Questo approccio presuppone che gli elementi riscaldanti possano mantenere la temperatura della parete definita.
Poiché si semplifica la radiazione esterna, questo modello non può prevedere se gli elementi riscaldanti sono effettivamente in grado di sostenere il profilo di temperatura richiesto sotto un pesante carico termico. Presuppone che la condizione al contorno sia assoluta.
Fare la scelta strategica di modellazione
Quando si decide come strutturare la simulazione termica, considerare gli obiettivi ingegneristici specifici:
- Se il tuo obiettivo principale è la qualità del processo interno: Utilizza questa condizione al contorno per analizzare la storia termica precisa del nastro e la sua interazione con l'ossigeno fluente.
- Se il tuo obiettivo principale è il dimensionamento delle attrezzature: Sfrutta la velocità di calcolo semplificata per iterare rapidamente sulla lunghezza ottimale del forno richiesta per il tuo processo.
Definendo correttamente questa condizione al contorno, trasformi il tubo di quarzo da una variabile a una costante, trasformando un complesso problema di fisica in uno strumento di progettazione gestibile.
Tabella Riassuntiva:
| Aspetto Strategico | Impatto sulla Simulazione | Beneficio per l'Ingegneria |
|---|---|---|
| Complessità Radiativa | Elimina i calcoli non lineari riscaldatore-tubo | Riduce i costi e i tempi computazionali |
| Focus del Modello | Disaccoppia il riscaldamento esterno dalla reazione interna | Consente un'analisi precisa dell'interazione nastro-ossigeno |
| Output di Progettazione | Fornisce chiari gradienti di temperatura | Determina la lunghezza ottimale del forno per la lavorazione |
| Tipo di Approccio | Ibrido (utilizza dati di input empirici) | Aumenta l'accuratezza della storia termica interna |
Lavorazione Termica di Precisione per la Tua Ricerca e Produzione
Sblocca il pieno potenziale dei tuoi esperimenti termici con KINTEK. Sia che tu stia modellando complessi trasferimenti di calore o scalando la produzione, i nostri sistemi ad alte prestazioni forniscono la coerenza che i tuoi dati richiedono.
Supportato da R&S e produzione esperte, KINTEK offre una gamma completa di attrezzature da laboratorio tra cui sistemi Muffle, Tube, Rotary, Vacuum e CVD. Tutti i nostri forni ad alta temperatura sono completamente personalizzabili per soddisfare le tue specifiche condizioni al contorno e requisiti di processo.
Pronto a ottimizzare i tuoi risultati termici? Contatta oggi i nostri esperti tecnici per trovare la soluzione di forno personalizzabile perfetta per il tuo laboratorio.
Guida Visiva
Riferimenti
- Zili Zhang, Qiuliang Wang. A Tube Furnace Design for the Oxygen Annealing of a REBCO Superconducting Joint. DOI: 10.3390/ma18133053
Questo articolo si basa anche su informazioni tecniche da Kintek Furnace Base di Conoscenza .
Prodotti correlati
- 1700℃ Forno tubolare da laboratorio ad alta temperatura con tubo in quarzo o allumina
- 1400℃ Forno tubolare da laboratorio ad alta temperatura con tubo in quarzo e allumina
- Forno tubolare al quarzo da laboratorio Forno tubolare riscaldante RTP
- 1200℃ Forno a tubo diviso Forno a tubo di quarzo da laboratorio con tubo di quarzo
- Forno tubolare al quarzo da laboratorio verticale Forno tubolare
Domande frequenti
- Come viene utilizzato un forno tubolare ad alta temperatura nella sintesi di nanocompositi MoO2/MWCNT? Guida di precisione
- Perché viene utilizzato un forno tubolare per il trattamento termico dei materiali catodici compositi S/C? Ottimizzare la stabilità della batteria
- Come far funzionare un forno tubolare? Una guida in 5 fasi per risultati sicuri e ripetibili
- Come viene utilizzato un forno a tubo verticale per studi sull'accensione delle polveri di combustibile? Modello di combustione industriale con precisione
- Come funziona un forno a tubo? Padroneggiare il controllo preciso del calore e dell'atmosfera
