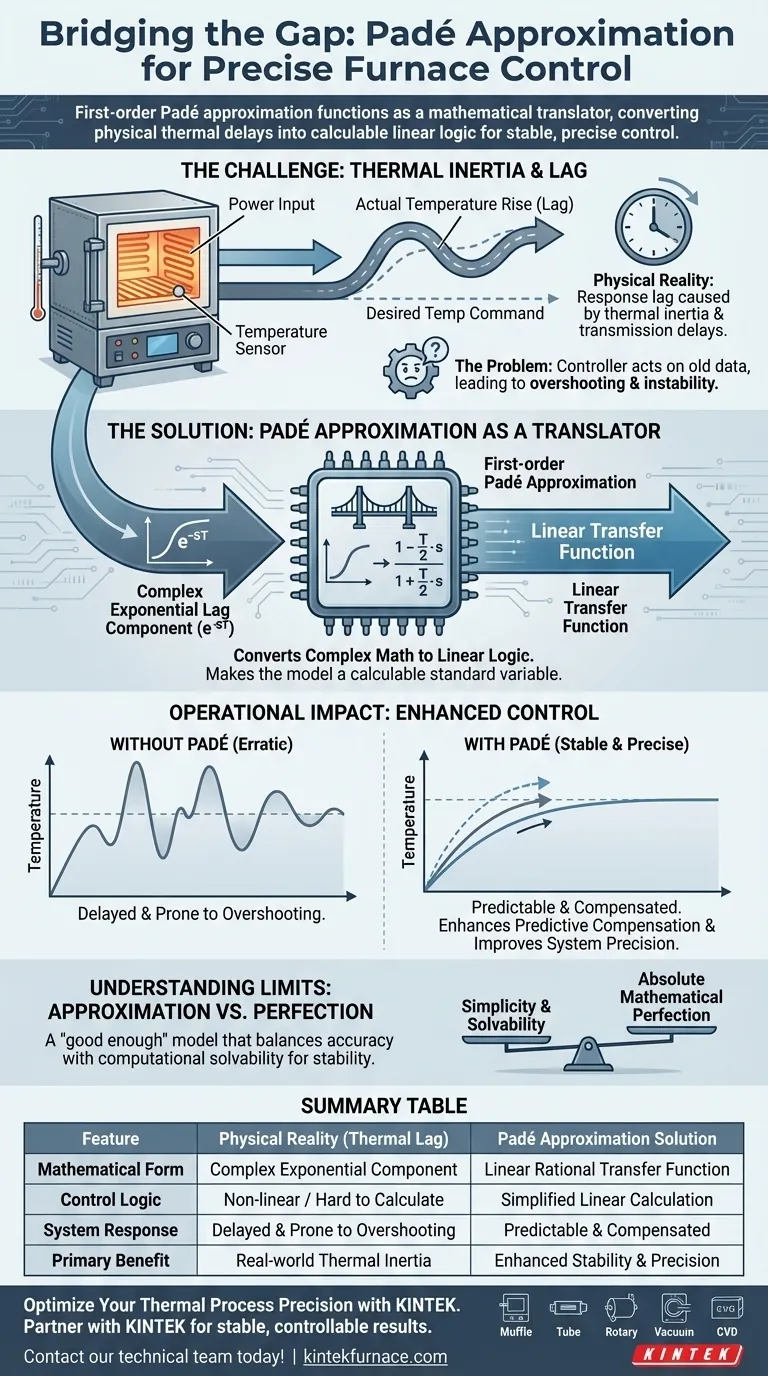
L'approssimazione di Padé del primo ordine funziona come un traduttore matematico che colma il divario tra i ritardi termici fisici e la logica del sistema di controllo. Affronta le sfide tecniche nella regolazione dei forni elettrici convertendo complessi componenti di ritardo esponenziale, causati dall'inerzia termica e dai ritardi di trasmissione, in una funzione di trasferimento lineare calcolabile. Questa trasformazione consente al controllore di compensare efficacemente i ritardi di risposta, garantendo che il sistema rimanga stabile e preciso.
I forni elettrici industriali possiedono un'inerzia termica significativa, creando ritardi temporali difficili da gestire per gli algoritmi standard. L'approssimazione di Padé del primo ordine semplifica questi complessi ritardi in un formato lineare, consentendo al sistema di controllo di prevedere il comportamento in modo affidabile e di mantenere una regolazione precisa della temperatura.
La Sfida: Inerzia Termica e Ritardo
La Realtà Fisica dei Forni Elettrici
In ambito industriale, i forni elettrici non rispondono istantaneamente alle variazioni di potenza. Esiste sempre un ritardo di risposta causato dall'inerzia termica e dai ritardi di trasmissione.
Il Problema dei Ritardi Temporali
Quando un controllore invia un segnale per aumentare il calore, l'effettivo aumento della temperatura avviene in seguito. Questo ritardo di trasmissione crea una disconnessione tra il comando e il risultato.
Senza un'adeguata modellazione, un controllore reagisce a dati obsoleti. Ciò porta spesso a superare la temperatura target o all'instabilità del sistema.
Come l'Approssimazione di Padé Risolve il Problema
Conversione di Matematica Complessa in Logica Lineare
Matematicamente, i ritardi temporali puri sono rappresentati come complessi componenti di ritardo esponenziale. Questi sono difficili da utilizzare direttamente nei calcoli standard dei loop di controllo lineari.
L'approssimazione di Padé del primo ordine risolve questo problema convertendo il termine esponenziale in una funzione di trasferimento lineare. Crea una frazione razionale matematica che approssima il ritardo.
Rendere il Modello Calcolabile
Una volta convertito, il ritardo diventa una parte gestibile dell'equazione del sistema. L'algoritmo di controllo può ora elaborare il ritardo come una variabile standard piuttosto che un'anomalia complessa.
Impatto Operativo sul Controllo della Temperatura
Miglioramento della Compensazione Predittiva
Linearizzando il ritardo, il controllore del forno può prevedere in modo più affidabile come reagirà la temperatura nel tempo. Può "vedere" il ritardo in arrivo e regolare in anticipo l'erogazione di potenza per compensare.
Miglioramento della Precisione e Stabilità del Sistema
Il risultato finale è un sistema più robusto. Poiché il controllore tiene conto accuratamente dell'inerzia termica, previene fluttuazioni erratiche.
Ciò porta a una maggiore precisione e stabilità durante il funzionamento effettivo, garantendo che il forno mantenga la temperatura corretta senza oscillazioni costanti.
Comprendere i Limiti dell'Approssimazione
Approssimazione vs. Perfezione
È importante ricordare che questo metodo è un'approssimazione, non una replica esatta del ritardo fisico. Semplifica la serie infinita di una funzione esponenziale in un rapporto lineare finito.
Bilanciare Semplicità e Accuratezza
Sebbene molto efficace per stabilizzare i loop standard dei forni, scambia la perfezione matematica assoluta con la solubilità computazionale. Fornisce un modello "abbastanza buono" per garantire la stabilità senza richiedere un'eccessiva potenza di elaborazione.
Fare la Scelta Giusta per la Tua Strategia di Controllo
Quando si progetta o si ottimizza un modello di controllo della temperatura per un forno elettrico, considerare come questa approssimazione si allinea ai propri obiettivi specifici.
- Se il tuo obiettivo principale è la Stabilità del Sistema: Utilizza l'approssimazione di Padé per prevenire oscillazioni causate dal ritardo tra l'elemento riscaldante e il sensore.
- Se il tuo obiettivo principale è la Semplicità dell'Algoritmo: Implementa questo metodo per convertire la complessa matematica del ritardo non lineare in una funzione lineare standard facile da calcolare.
Convertendo il ritardo fisico in un valore matematico lineare, trasforma una risposta termica caotica in un processo prevedibile e controllabile.
Tabella Riassuntiva:
| Caratteristica | Realtà Fisica (Ritardo Termico) | Soluzione con Approssimazione di Padé |
|---|---|---|
| Forma Matematica | Componente Esponenziale Complesso | Funzione di Trasferimento Razionale Lineare |
| Logica di Controllo | Non lineare / Difficile da Calcolare | Calcolo Lineare Semplificato |
| Risposta del Sistema | Ritardata e soggetta a Overshooting | Prevedibile e Compensata |
| Beneficio Principale | Inerzia Termica del Mondo Reale | Maggiore Stabilità e Precisione |
Ottimizza la Precisione del Tuo Processo Termico con KINTEK
Superare l'inerzia termica richiede sia precisione matematica che hardware ad alte prestazioni. KINTEK fornisce soluzioni di riscaldamento all'avanguardia supportate da ricerca e sviluppo e produzione esperti. Sia che tu richieda sistemi Muffle, Tube, Rotary, Vacuum o CVD, i nostri forni ad alta temperatura da laboratorio sono completamente personalizzabili per soddisfare le tue esigenze uniche di regolazione della temperatura.
Non lasciare che i ritardi di risposta compromettano i tuoi risultati. Collabora con KINTEK per ottenere la stabilità e il controllo che la tua ricerca richiede. Contatta oggi il nostro team tecnico per discutere le tue esigenze di forni personalizzati!
Guida Visiva
Riferimenti
- Serdar Ekinci, Євген Зайцев. Efficient control strategy for electric furnace temperature regulation using quadratic interpolation optimization. DOI: 10.1038/s41598-024-84085-w
Questo articolo si basa anche su informazioni tecniche da Kintek Furnace Base di Conoscenza .
Prodotti correlati
- Forno ad atmosfera inerte controllata con azoto da 1200℃
- 1700℃ Forno ad atmosfera inerte controllata con azoto
- Forno ad atmosfera inerte controllata con azoto da 1400℃
- 1200℃ Forno a tubo diviso Forno a tubo di quarzo da laboratorio con tubo di quarzo
- Forno di sinterizzazione al plasma di scintilla SPS
Domande frequenti
- Qual è lo scopo principale del trattamento termico? Trasformare le proprietà dei metalli per prestazioni superiori
- Quali sono i vantaggi del trattamento termico in atmosfera inerte? Prevenire l'ossidazione e preservare l'integrità del materiale
- A cosa serve l'azoto in un forno? Prevenire l'ossidazione e controllare la qualità del trattamento termico
- Come funziona un forno a atmosfera controllata di tipo batch? Trattamento Termico di Precisione Superiore per Materiali Eccellenti
- Quali sono i vantaggi principali di un forno a atmosfera sperimentale a scatola? Ottenere un controllo ambientale preciso per materiali avanzati
